Interpréter les résultats d'une régression linéaire : 4 scénarios

La régression linéaire est l'un des outils statistiques les plus couramment utilisés pour modéliser la relation entre une variable d'intérêt (variable dépendante, Y) et une variable explicative (X). Mais une question revient souvent : quels indicateurs faut-il privilégier pour analyser la qualité et l'interprétation du modèle ?

Dans cet article, nous allons explorer 4 scénarios différents et voir comment l'interprétation d'une régression linéaire peut varier en fonction de trois critères clés :

• La proportion de variance expliquée (R²) : mesure dans quelle mesure le modèle explique les variations de Y.

• La p-value associée à la pente : permet d'évaluer la significativité statistique de la relation.

• La taille de la pente : renseigne sur l'ampleur de l'effet de X sur Y.

Contexte de l'exemple

Imaginons que nous étudions l'effet d'un dosage de marqueur biologique (X) sur un résultat clinique (Y). Nous disposons de mesures sur une cohorte de patients et nous ajustons une régression linéaire simple pour examiner cette relation.

Nous allons examiner quatre scénarios illustrant différentes combinaisons de R², p-value et pente.

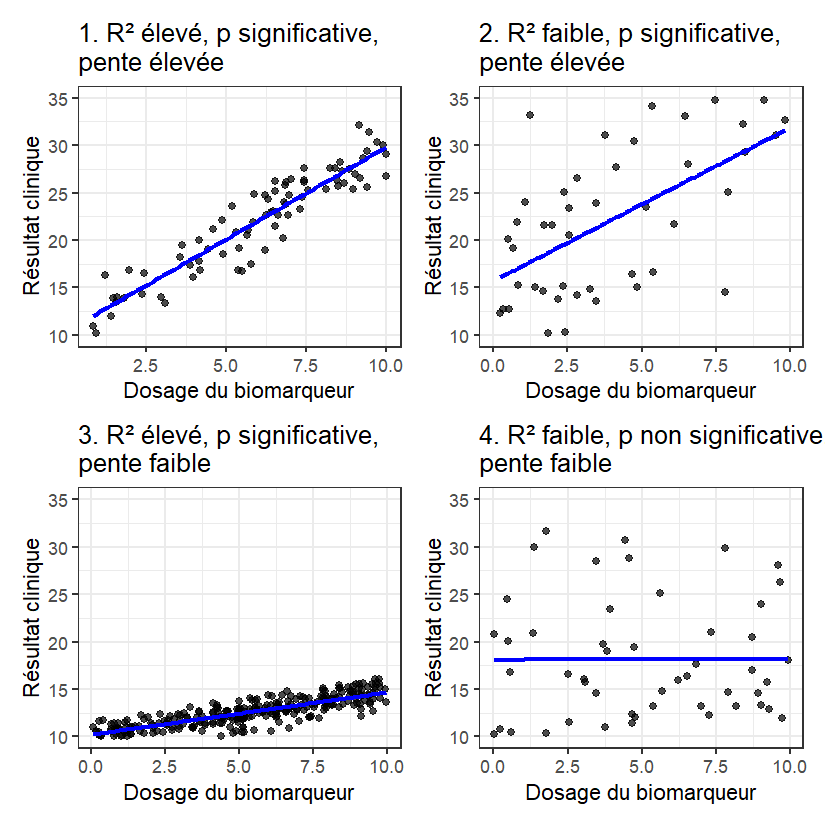
1. R² élevé, p-value significative, pente forte

Interprétation :

• R² = 0.8 : 80% de la variabilité du résultat clinique est expliquée par le marqueur biologique. Le modèle ajuste bien les données.

• p-value significative : il existe une relation statistiquement significative entre X et Y.

• Pente = 2 : chaque augmentation de 1 unité du marqueur est associée à une augmentation de 2 unités du résultat clinique.

👉 Ce scénario est idéal : le modèle prédit bien Y, la relation est significative et l'effet est clair.

2. R² faible, p-value significative, pente forte

Interprétation :

• R² = 0.5 : seulement 50% de la variabilité de Y est expliquée par X, ce qui suggère que d'autres variables influencent fortement le résultat clinique.

• p-value significative : la relation est bien statistiquement significative.

• Pente = 3.5 : une augmentation de 1 unité du marqueur biologique entraine une augmentation importante du résultat clinique.

👉 Malgré un R² faible, ce modèle pourrait suffire si notre objectif est simplement d'établir une association entre X et Y sans chercher à expliquer toute la variabilité de Y.

3. R² élevé, p-value significative, pente faible

Interprétation :

• R² = 0.7 : X explique une grande partie de la variabilité de Y.

• p-value significative : la relation est statistiquement confirmée.

• Pente = 0.5 : l'effet de X sur Y est très faible. Une augmentation de 1 unité de X n'entraîne qu'une très petite augmentation de Y.

👉 Dans ce cas, même si la relation est significative et que X prédit bien Y, la taille de l'effet est faible. Il faut alors se demander si cette augmentation de Y est pertinente cliniquement.

4. R² faible, p-value non significative, pente faible

Interprétation :

• R² faible : X n'explique pratiquement pas la variabilité de Y.

• p-value non significative : pas de relation statistique détectée.

• Pente faible : X n'a qu'un très faible effet sur Y.

👉 Ici, il n'y a pas de lien évident entre X et Y. Ce scénario suggère que X n'est pas une variable pertinente pour expliquer Y.

Synthèse et recommandations

🔹 R² élevé et p-value significative sont idéaux, mais il faut aussi prendre en compte la taille de l'effet.

🔹 Une p-value significative avec un R² faible peut suffire si l'objectif est uniquement de prouver une association, mais il ne faut pas surinterpréter la pente.

🔹 Une pente faible avec une p-value significative demande de se poser la question de la pertinence clinique.

🔹 Un R² faible et une p-value non significative indiquent qu'il vaut mieux explorer d'autres variables explicatives.